Artificial Neural Networks: Architectures

Not all Artificial Neural Networks (ANN) are made the same, each is designed to tackle a specific type of problem. In this note, we’ll explore the most prominent architectures in detail, and learn how they are used in different applications.

What about Transformers? At the time of writing of this note, the Transformer architecture has not taken over the ANN world yet. Instead of updating this note with new information, we look at Transformers in a lot more detail in a subsequent note.

Feedforward Neural Networks (FNNs)

In FNNs, the information moves only in the forward direction, from the inputs to the output layer. This makes FNNs the simplest ANN architecture. There is no cycling or looping back of information, which simplifies the learning process. We had an in-depth look at FNN structure in our discussion of the ANN Basics.

FNNs are commonly used in cases where the output is expected from a set of inputs, such as image classification, customer classification for marketing, and more. A typical application is in handwriting recognition, where the input layer receives pixel data, and the output layer classifies the data into various categories like letters or numbers.

Convolutional Neural Networks (CNNs)

CNNs are particularly tailored for grid-like data interpretation. They employ layers of convolutions whereby filters are applied to the original data to create feature maps that summarize key features of the data.

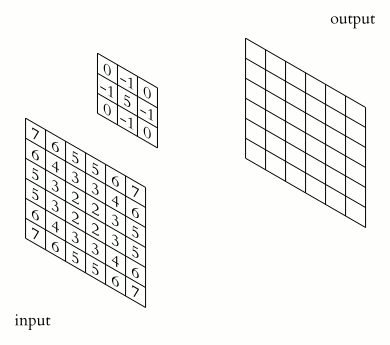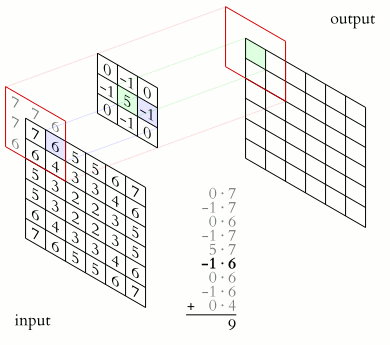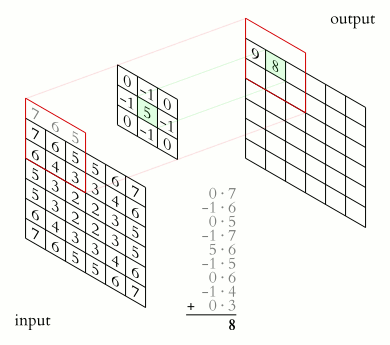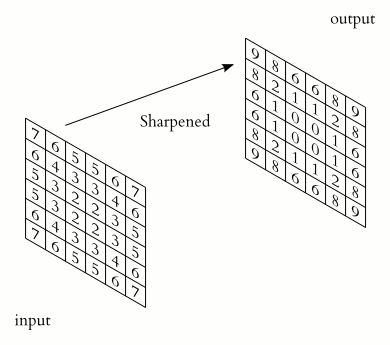
The filters, also known as kernels, are essentially small weight matrices that CNNs learn during the training process. These filters are applied to the input data through a mathematical operation called convolution, which essentially measures the similarity between the filter and local regions of the input data.

During convolution, a filter is slid across the input image. At each position, the filter is element-wise multiplied by the values of the image it covers. The results of these multiplications are summed up to produce a single number in the output feature map for that filter at that location. The output of applying a filter across the entire input is called a feature map or activation map. This feature map represents specific features of the input data, detected by the filter. Different filters can detect edges, textures, colors, or other visual elements depending on what the filter has learned during training.

Nerd Moment: Convolution or Cross-correlation?

In mathematical terms, the convolution operation performed on two functions involves the flipping (reflection) of one of the functions by a change of sign for the inputs. This operation allows the convolution operation to be commutative. In most CNNs, this reflection is not applied, which technically means that CNNs don’t really use the convolution operation, but instead rely on a similar operation called cross-correlation.

Initially, the values in the filters are set randomly. However, through backpropagation training, these values are adjusted to help the network minimize the error in its predictions. As the network trains, filters automatically learn to capture relevant features that are most useful for performing the task at hand, whether it’s recognizing faces, identifying objects, or classifying scenes.

In the initial layers of a CNN, filters typically learn to detect low-level features such as edges, gradients, and simple textures. As we progress deeper into the network, the filters start detecting more complex features such as parts of objects (e.g., wheels, eyes, leaves). In the deeper layers, filters combine the earlier detected features to recognize high-level, more abstract features like entire objects or complex scenes.

In addition to image and video recognition, CNNs are also used in natural language processing (e.g., sentence classification) and other areas requiring recognition of patterns in spatial data.

Recurrent Neural Networks (RNNs)

RNNs introduce loops in the network architecture, allowing information to persist. This structure is crucial for handling sequential data of arbitrary size, where the current output depends not just on the current input but also on the previous ones. In essence, their architecture allows them to maintain a form of memory by using their output or state as input for the next step in the sequence. This makes RNNs particularly well-suited for tasks where the sequence of data points is important, such as time series prediction, natural language processing, speech recognition, and music processing. RNNs (in their true form) are essentially directed cyclic graphs.

The basic unit within an RNN layer is a cell. The simplest form of an RNN cell has a structure similar to a standard neural network layer, plus a connection from the output of the cell back to its input.

At each time step \( t \), the RNN takes two inputs: the current data point \( x_t \) from the sequence and the hidden state from the previous time step \( h_{t-1} \). The hidden state \( h_{t-1} \) serves as the “memory” of the network, containing information about the previous elements of the sequence. The cell uses these inputs to calculate the new hidden state \( h_t \), which will be used in the next time step and can also be used to generate an output \( y_t \).

The hidden state \( h_t \) is updated using a non-linear function \( f \), often a tanh or sigmoid function, which combines the input \( x_t \) and the previous hidden state \( h_{t-1} \) as follows:

$$ h_t = f(W_{hh} h_{t-1} + W_{xh} x_t + b_h) $$

Here, \( W_{hh} \) and \( W_{xh} \) are weights applied to the previous hidden state and the current input, respectively, and \( b_h \) is a bias term.

The output \( y_t \) at each time step can be calculated using the hidden state \( h_t \), often with another function \( g \), typically a softmax for classification tasks:

$$ y_t = g(W_{hy} h_t + b_y) $$

where \( W_{hy} \) is the weight matrix for the output, and \( b_y \) is the output bias.

Despite their effectiveness for sequential data, RNNs face significant challenges:

• Vanishing Gradient Problem: As gradients are propagated backward through each time step in the sequence, they can become extremely small (vanish), making it difficult to learn long-range dependencies within the sequence data.
• Exploding Gradients: Conversely, gradients can also grow exponentially, leading to very large updates to model weights and resulting in an unstable network.

To address these issues, several variants of RNNs have been developed:

• Long Short-Term Memory (LSTM): LSTMs include mechanisms called gates that control the flow of information. These gates help the network retain or forget information, effectively addressing the vanishing gradient problem.
• Gated Recurrent Unit (GRU): GRUs are a simpler alternative to LSTMs that use a similar gating concept but with fewer parameters.

RNNs excel in language modeling, speech recognition, and any other application that requires the interpretation of sequential data. In text generation, RNNs can predict the next character or word in a sequence based on the previous characters or words.

Autoencoders

Comprising an encoder and a decoder, autoencoders first compress the input into a latent-space representation and then reconstruct the output from this representation. The goal is typically to learn a compressed representation of the data. Typically used in anomaly detection, noise reduction, and data denoising, where the network learns to ignore the noise and reconstruct the original input. Training of autoencoders essentially involves unsupervised representation learning. They are designed to learn efficient codings of unlabeled data, often for the purposes of dimensionality reduction or feature extraction.

An autoencoder consists of two main parts:

1. Encoder: This part of the network compresses the input into a smaller, encoded representation. The encoder is typically formed by a series of layers that gradually decrease in size, funneling the input data into a more compact form.

2. Decoder: This part of the network attempts to reconstruct the input data from the encoded representation. The decoder mirrors the encoder, with layers that gradually increase in size, culminating in an output layer that matches the dimensions of the input data.

Autoencoders are trained through a process that involves optimizing the parameters of the encoder and decoder so that the output (reconstructed input) closely matches the original input. During the forward pass, an input batch of data is passed through the encoder, which compresses it into a smaller, dense representation (often called the “latent space” or “encoding”). This encoding is then fed into the decoder, which attempts to reconstruct the original input from this compressed form. After the forward pass, the reconstruction is compared to the original input to calculate the loss, which quantifies the difference between the two. The loss calculated from the output is then used to perform backpropagation.

There are various types of autoencoders:

• Standard Autoencoders: Focus on minimizing the reconstruction error between the input and the output.
• Variational Autoencoders (VAEs): These introduce a probabilistic approach to the encoding process, producing a distribution over the possible inputs. They are used extensively in generative models.
• Denoising Autoencoders: Specifically designed to remove noise from the input during the encoding process, thus learning to recover the original undistorted input.
• Sparse Autoencoders: Incorporate a sparsity constraint on the hidden layers to induce a lower capacity representation, thereby learning more robust features of the data.

Autoencoders are used in a variety of applications:

• Dimensionality Reduction: Similar to PCA, autoencoders can reduce the dimensionality of data, making it easier to visualize or process.
• Feature Learning: Can automatically learn the features to be used for further machine learning or data analysis tasks.
• Anomaly Detection: By learning to reproduce only the common patterns in the data, autoencoders can be used to detect outliers or anomalous data points.
• Image Reconstruction and Denoising: Useful in image processing tasks to enhance the quality of images or remove noise.

Generative Adversarial Networks (GANs)

A GAN consists of two competing neural network models. A generator creates samples intended to come from the same distribution as the training data, and a discriminator evaluates them against the real data, learning to differentiate between the two. GANs use two neural networks, pitting one against the other (thus the “adversarial”) to generate new, synthetic instances of data that can pass for real data. They are widely used in applications such as image generation, video generation, and more sophisticated machine learning tasks where synthesizing new data is beneficial.

GANs consist of two distinct models, each with its own role:

1. Generator: This model learns to generate plausible data. The generated instances become more realistic over the course of training. The generator starts with a random noise vector (seed) and transforms this seed into data with the same dimensions as the training set.

2. Discriminator: This model is a classifier that learns to distinguish between real and synthetic data. The goal of the discriminator is to accurately predict whether a given data instance is real (from the training set) or fake (created by the generator).

The training of GANs involves an iterative, adversarial process where the generator and the discriminator compete against each other. It is a delicate process that involves balancing the performance of the two models. Here’s how the process generally works:

• The discriminator is trained for a set number of iterations first. This training involves presenting it with samples from the training data (real) and samples of faked data.
• The discriminator’s job is to output the probability that the received data is real. Training consists of maximizing the probability of correctly labeling both real and fake data.
• The generator is trained to produce data that the discriminator will classify as real. This is typically done by using the gradients of the discriminator’s predictions to update the generator’s weights.
• Essentially, the generator is rewarded for fooling the discriminator.

Common challenges in training GANs include:

• Mode Collapse: Sometimes, the generator finds and exploits weaknesses in the discriminator’s strategy, leading to the generator producing limited varieties of outputs.
• Failure to Converge: The adversarial nature can sometimes lead to training stability issues, where neither model reaches a point where it can no longer improve because any change would lessen its performance.
• Vanishing Gradients: This can occur when the discriminator gets too good, which results in the generator gradient vanishing and thus no longer updating effectively.

GANs are widely used in image generation, video game content creation, fashion and design, drug discovery, and even in enhancing space exploration images by generating high-resolution versions of pixelated images.

Wrap-up

Each of these architectures leverages unique properties suited to specific tasks, from processing individual data points in isolation to handling inputs where context and order significantly impact the output. As the field of AI progresses, the development of these and newer architectures will continue to be central to overcoming the challenges posed by complex data and diverse applications… unless Transformers get invented and make most of these architectures obsolete.